AI and Memory Wall
Update: An extended version of this blogpost is published in IEEE Micro Journal and is available online here.
(This blogpost has been written in collaboration with Zhewei Yao, Sehoon Kim, Michael W. Mahoney, and Kurt Keutzer. The data used for this study is available online.).
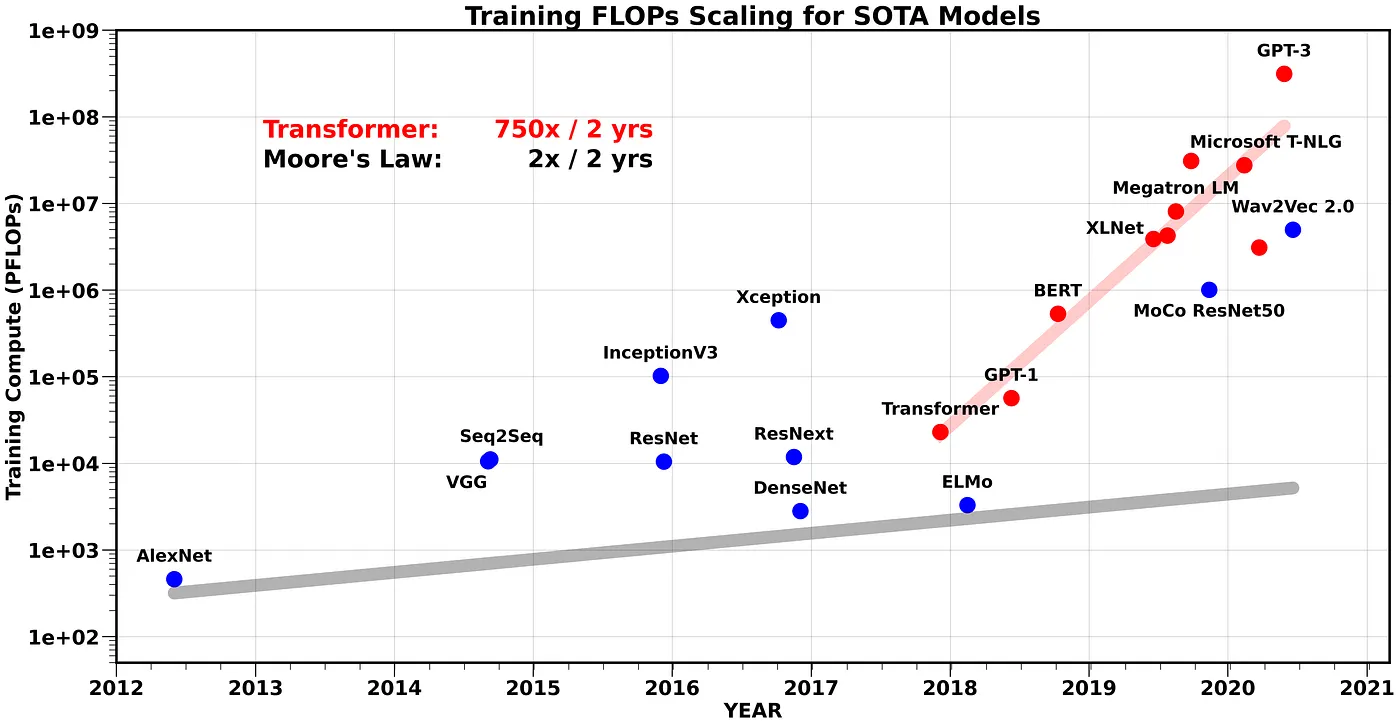
The amount of compute needed to train SOTA Transformer models, has been growing at a rate of 750x/2yrs. This exponential trend has been the main driver for AI accelerators that focus on increasing the peak compute power of hardware, often at the expense of simplifying and/or removing other parts such as memory hierarchy.
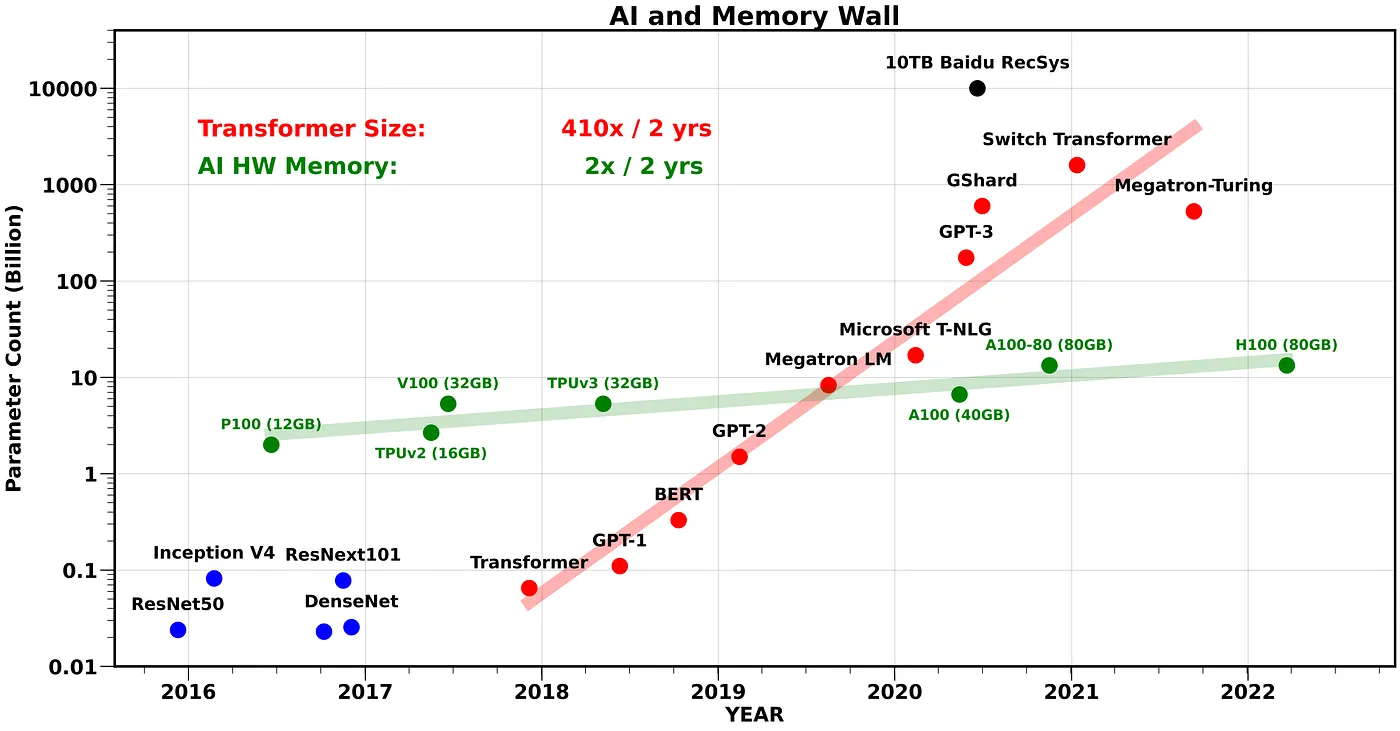
However, these trends miss an emerging challenge with training and serving these models: memory and communication bottlenecks. In fact, several AI applications are becoming bottlenecked by intra/inter-chip and communication across/to AI accelerators rather than compute. In particular, the flagship LLM model sizes has been increasing at a rate of 410x every 2 years. See Figure 2. Similarly, Large Recommendation System models have reached O(10) TB parameters. Contrast this with accelerator DRAM memory, which has only scaled at a rate of 2x every 2 years.
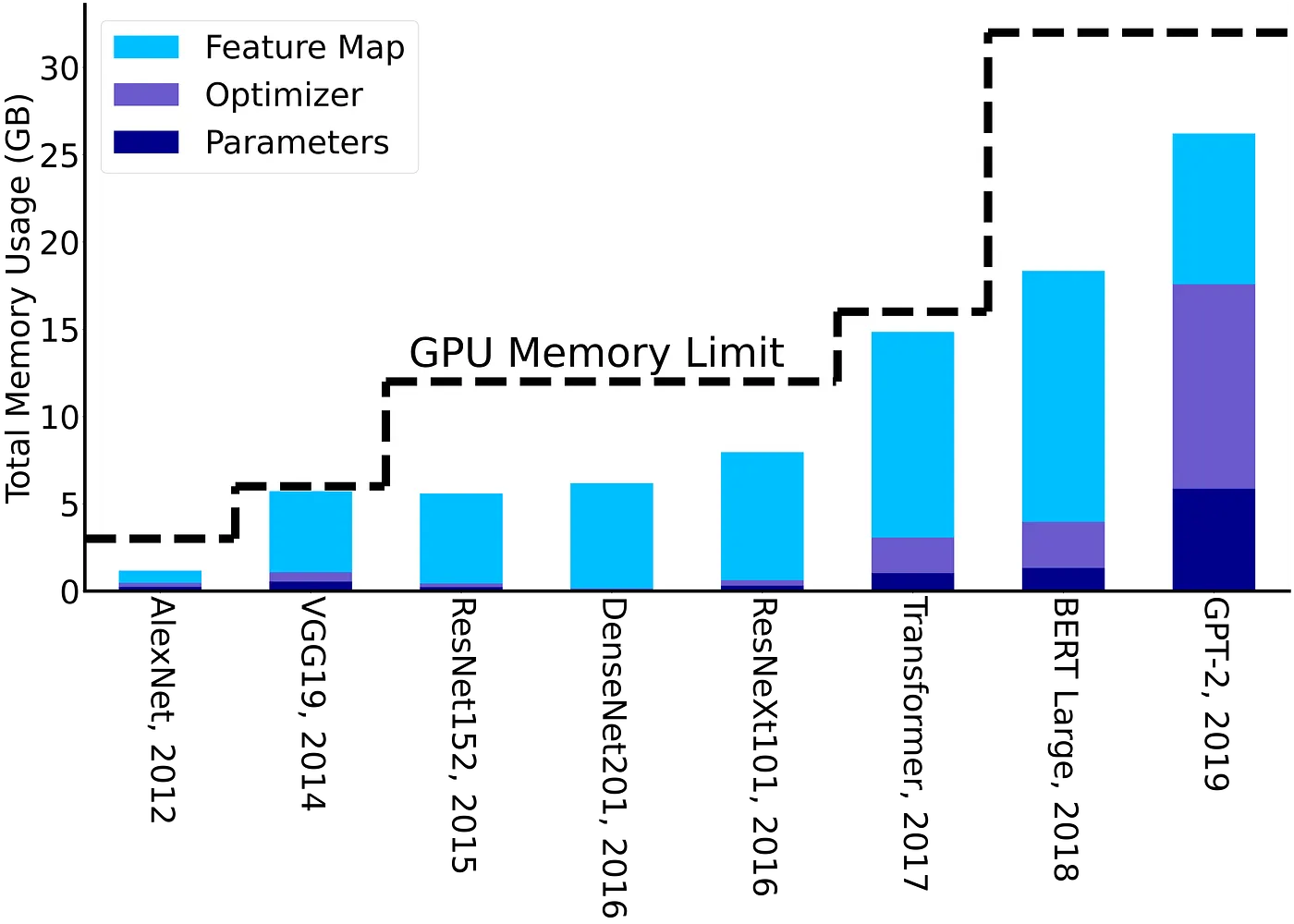
It is important to note that the memory requirements to train AI models are typically several times larger than the number of parameters. This is because training requires storing intermediate activations, and this typically adds 3–4x more memory than the number of parameters (excluding embeddings). This is illustrated in Figure 3, where the total training memory footprint is shown for training different flagship AI models throughout the years. We can clearly see how the design of SOTA Neural Network (NN) models has been implicitly influenced by the DRAM capacity of the accelerators in different years.
These challenges are commonly referred to as the memory wall problem, a term originally coined by William Wulf and Sally Mckee in 1995 [25]. The memory wall problem involves both the limited capacity and the bandwidth of memory transfer. This entails different levels of memory data transfer. For example, data transfer between compute logic and on-chip memory, or between compute logic and DRAM memory, or across different processors on different sockets. For all these cases, the capacity and the speed of data transfer has been significantly lagging behind hardware (HW) compute capabilities.
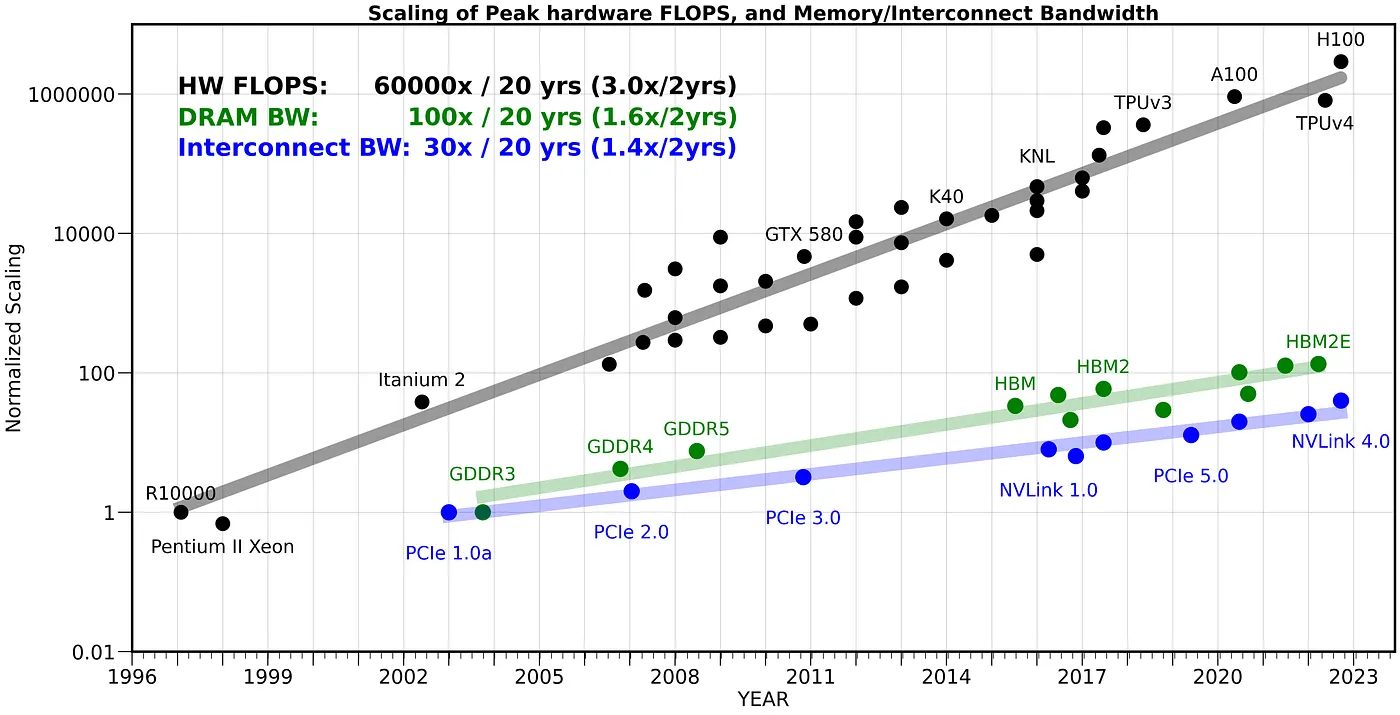
One might hope that we can use distributed-memory parallelism by scaling-out the training to multiple accelerators to avoid the single HW’s limited memory capacity and bandwidth. However, distributing the work over multiple processes also faces the memory wall problem: the communication bottleneck of moving data between NN accelerators, which is even slower and less efficient than on-chip data movement. Similar to the single system memory case, we have not been able to overcome the technological challenges to scale the network bandwidth. This can be seen from Figure 4, where we show how the peak compute has increased by 60,000x over the past 20 years, as opposed to 100x for DRAM or 30x for interconnect bandwidth. Unfortunately, it has been very difficult to overcome the fundamental challenges of increasing DRAM/Interconnect bandwidth [1]. As such, scale-out only works for highly compute-bound problems with very little communication and data transfer.
Promising Solutions for Breaking the Wall:
“No exponential can continue forever,” and delaying an exponential scaling at the rate of 410x/2yrs is not going to be feasible for long, even for large hyperscalar companies. This coupled with the increasing gap between compute and bandwidth capability will soon make it very challenging to train larger models, as the cost will be exponentially higher.
To continue the innovations and break the memory wall, we need to rethink the design of AI models. There are several issues here. First, the current methods for designing AI models are mostly ad-hoc, and/or involve very simple scaling rules. For instance, recent large Transformer models are mostly just a scaled version of almost the same base architecture proposed in the original BERT model [22]. Second, we need to design more data efficient methods for training AI models. Current NNs require a huge amount of training data and hundreds of thousands of iterations to learn, which is very inefficient. Some might note that it is also different from how human brains learn, which often only require very few examples per concept/class. Third, the current optimization and training methods need a lot of hyperparameter tuning (such as learning rate, momentum, etc.), which often results in hundreds of trial and error sweeps to find the right setting to train a model successfully. As such, the training cost reported in Figure 1 is only a lower bound of the actual overhead, and the true cost is typically much higher. Fourth, the prohibitive size of the SOTA NN models makes their deployment for inference very challenging. This is not just restricted to models such as GPT-3. In fact, deploying large recommendation systems (which are similar to Transformers but which have much larger embedding and very few MLP layers afterwards [23]) that are used by hyperscalar companies is a major challenge. Finally, the design of hardware accelerators has been mainly focused on increasing peak compute with relatively less attention on improving memory-bound workloads. This has made it difficult both to train large models, as well as to explore alternative models, such as Graph NNs which are often bandwidth-bound and cannot efficiently utilize current accelerators.
All of these issues are fundamental problems in machine learning. Here, we briefly discuss recent research (including some of our own) that has targeted the last three items.
Efficient Training Algorithms
One of the main challenges with training NN models is the need for brute-force hyperparameter tuning. This includes finding the learning rate, its annealing schedule, the number of iterations needed to converge, etc. This adds (much) more overhead for training SOTA models. Many of these problems arise from the first-order SGD methods used for training. While SGD variants are easy to implement, they are not robust to hyperparameter tuning, and are very hard to tune for new models for which the right set of hyperparameters are unknown. One promising approach to address this is to use second-order stochastic optimization methods such, as in our recently-developed ADAHESSIAN method [4]. These methods are typically more robust to hyperparameter tuning, and they can achieve SOTA. However, current methods have 3–4x higher memory footprint, which needs to be addressed. A promising line of work for that is the Zero paper from Microsoft, which showed how one can train 8x bigger models with the same memory capacity by removing/sharding redundant optimization state variables [21, 3]. If the overhead of these higher-order methods could be addressed, then they can signficantly reduce the total cost of training large models.
Another promising approach includes reducing the memory footprint and increasing the data locality of optimization algorithms, at the expense of performing more computations. One simple example is to only store/checkpoint a subset of activations during the forward pass, instead of saving all activations, to reduce the feature map’s memory footprint shown in Figure 3. The rest of the activations could then be recomputed when needed. Even though this will increase compute, one can significantly reduce the memory footprint by up to 5x [2] with just 20% more compute.
Another important solution is to design optimization algorithms that are robust to low precision training. In fact, one of the major breakthroughs in AI accelerators has been the use of half-precision (FP16) arithmetic, instead of single precision [5,6]. This has enabled more than 10x increase in hardware compute capability. However, it has been challenging to further reduce the precision from half-precision to INT8 without accuracy degradation with current optimization methods.
Efficient Deployment
Deploying recent SOTA models such as GPT-3 or large recommendation systems is quite challenging, as they require distributed-memory deployment for inference. One promising solution to address this is to compress these models for inference, by reducing the precision (i.e., quantization) or removing (i.e., pruning) their redundant parameters.
The first approach is quantization, a method that can be applied at the training and/or inference steps. While it has been very challenging to reduce the training precision much below FP16, it is possible to use ultra-low precision for inference. With current methods, it is relatively easy to quantize inference down to INT4 precision, with minimal impact on accuracy. This results in up to 8x reduction in model footprint and latency [7,8,19,20]. However, inference with sub-INT4 precision is more challenging and is currently a very active area of research.
Another possibility is to completely remove/prune redundant parameters in the model. With current methods, it is possible to prune up to 30% of neurons with structured sparsity, and up to 80% with unstructured sparsity, with minimal impact on accuracy [9,10]. Pushing beyond this limit, however, is very challenging, and it often results in fatal accuracy degradation. Resolving this is an open problem.
Rethinking the Design of AI Accelerators
There are fundamental challenges in increasing both the memory bandwidth and the peak compute capability of a chip at the same time [1]. However, it is possible to sacrifice peak compute to achieve better compute/bandwidth trade-offs. This is not an impossible task, and in fact, the CPU architecture already incorporates a well-optimized cache hierarchy. This is why CPUs have much better performance than GPUs for bandwidth-bound problems. Such problems include large recommendation problems. However, the main challenge with today’s CPUs is that their peak compute capability (i.e., FLOPS) is about an order of magnitude less than AI accelerators such as GPUs or TPUs. One reason for this is that AI accelerators have mainly been designed to achieve maximum peak compute. This often requires removing components such as cache hierarchy in favor of adding more compute logic. One could imagine an alternative architecture in between these two extremes, preferably with more efficient caching, and importantly with higher capacity DRAM (possibly a hierarchy of DRAMs with different bandwidths). The latter could be very helpful in mitigating the distributed-memory communication bottlenecks [18].
Conclusion
The computational cost of training recent SOTA Transformer models in NLP has been scaling at a rate of 750x/2yrs, and the model parameter size has been scaling at 400x/2yrs. In contrast, the peak hardware FLOPS is scaling at a rate of 3x/2yrs, while both the DRAM and interconnect bandwidth have been increasingly falling behind, with a scaling rate of 1.6x/2yrs and 1.4x/2yrs, respectively. To put these numbers into perspective, peak hardware FLOPS has increased by 60,000x over the past 20 years, while DRAM/Interconnect bandwidth has only scaled by a factor of 100x/30x over the same time period. With these trends, memory — in particular, intra/inter-chip memory transfer — will soon become the main limiting factoring in training large AI models. As such, we need to rethink the training, deployment, and design of AI models as well as how we design AI hardware to deal with this increasingly challenging memory wall.
We would like to thank Suresh Krishna, and Aniruddha Nrusimha for their valuable feedback.
[Update]: This article was updated on Sep, 2, 2023 with newer hardware and model data available.
*¹ We are specifically not including the cost of training Reinforcement Learning models in this graph, as the training cost is mostly related to the simulation environment and there is currently no consensus on a standard simulation environment. Also note that we report the PFLOPs required to train each model to avoid using any approximation for hardware deployment utilization, as the latter depends on the specific library and the hardware used. Finally, all the rates in this document have been computed by solving a linear regression to fit the data shown in each graph.
*² The growth rate shown in Figure 2 is calculated by only considering the Transformer based models (blue circles), and not the recommendation systems.
*³ The GPU memory is plotted by dividing the corresponding memory size by 6 as an approximate upper bound for the largest model that can be trained with the corresponding capacity.
*⁴ We are normalizing hardware peak FLOPS with the R10000 system, as it was used to report the cost of training Lenet-5 in the seminal work of [24].
REFERENCES:
[1] Patterson DA. Latency lags bandwidth. Communications of the ACM. 2004 Oct 1;47(10):71–5.
[2] Jain P, Jain A, Nrusimha A, Gholami A, Abbeel P, Keutzer K, Stoica I, Gonzalez JE. Checkmate: Breaking the memory wall with optimal tensor rematerialization. arXiv preprint arXiv:1910.02653. 2019 Oct 7.
[3] Rajbhandari S, Rasley J, Ruwase O, He Y. Zero: Memory optimizations toward training trillion parameter models. InSC20: International Conference for High Performance Computing, Networking, Storage and Analysis 2020 Nov 9 (pp. 1–16). IEEE.
[4] Yao Z, Gholami A, Shen S, Keutzer K, Mahoney MW. ADAHESSIAN: An adaptive second order optimizer for machine learning. arXiv preprint arXiv:2006.00719. 2020 Jun 1.
[5] Ginsburg B, Nikolaev S, Kiswani A, Wu H, Gholaminejad A, Kierat S, Houston M, Fit-Florea A, inventors; Nvidia Corp, assignee. Tensor processing using low precision format. United States patent application US 15/624,577. 2017 Dec 28.
[6] Micikevicius P, Narang S, Alben J, Diamos G, Elsen E, Garcia D, Ginsburg B, Houston M, Kuchaiev O, Venkatesh G, Wu H. Mixed precision training. arXiv preprint arXiv:1710.03740. 2017 Oct 10.
[7] Yao Z, Dong Z, Zheng Z, Gholami A, Yu J, Tan E, Wang L, Huang Q, Wang Y, Mahoney MW, Keutzer K. HAWQV3: Dyadic Neural Network Quantization. arXiv preprint arXiv:2011.10680. 2020 Nov 20.
[8] Gholami A, Kim S, Yao Z, Dong Z, Mahoney M, Keutzer K, A Survey of Quantization Methods for Efficient Neural Network Inference, arxiv preprint, arxiv:arXiv:2103.13630, 2021.
[9] Gale T, Elsen E, Hooker S. The state of sparsity in deep neural networks. arXiv preprint arXiv:1902.09574. 2019 Feb 25.
[10] Hoefler T, Alistarh D, Ben-Nun T, Dryden N, Peste A. Sparsity in Deep Learning: Pruning and growth for efficient inference and training in neural networks. arXiv preprint arXiv:2102.00554. 2021 Jan 31.
[11] Iandola FN, Han S, Moskewicz MW, Ashraf K, Dally WJ, Keutzer K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv preprint arXiv:1602.07360. 2016 Feb 24.
[12] Gholami A, Kwon K, Wu B, Tai Z, Yue X, Jin P, Zhao S, Keutzer K. Squeezenext: Hardware-aware neural network design. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops 2018 (pp. 1638–1647).
[13] Wu B, Iandola F, Jin PH, Keutzer K. Squeezedet: Unified, small, low power fully convolutional neural networks for real-time object detection for autonomous driving. InProceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops 2017 (pp. 129–137).
[14] Shaw A, Hunter D, Landola F, Sidhu S. SqueezeNAS: Fast neural architecture search for faster semantic segmentation. InProceedings of the IEEE/CVF International Conference on Computer Vision Workshops 2019.
[15] Wu B, Wan A, Yue X, Keutzer K. Squeezeseg: Convolutional neural nets with recurrent crf for real-time road-object segmentation from 3d lidar point cloud. In2018 IEEE International Conference on Robotics and Automation (ICRA) 2018 May 21 (pp. 1887–1893). IEEE.
[16] Iandola FN, Shaw AE, Krishna R, Keutzer KW. SqueezeBERT: What can computer vision teach NLP about efficient neural networks?. arXiv preprint arXiv:2006.11316. 2020 Jun 19.
[17] Howard AG, Zhu M, Chen B, Kalenichenko D, Wang W, Weyand T, Andreetto M, Adam H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861. 2017 Apr 17.
[18] Krishna S, Krishna R. Accelerating Recommender Systems via Hardware” scale-in”. arXiv preprint arXiv:2009.05230. 2020 Sep 11.
[19] Kim S, Gholami A, Yao Z, Mahoney MW, Keutzer K. I-BERT: Integer-only BERT Quantization. arXiv preprint arXiv:2101.01321. 2021 Jan.
[20] Patrick Judd, Senior Deep Learning Architect, Integer Quantization for DNN Acceleration, Nvidia, GTC 2020.
[21] Bottou L, Curtis FE, Nocedal J. Optimization methods for large-scale machine learning. Siam Review. 2018;60(2):223–311.
[22] Devlin J, Chang MW, Lee K, Toutanova K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. 2018 Oct 11.
[23] Naumov M, Mudigere D, Shi HJ, Huang J, Sundaraman N, Park J, Wang X, Gupta U, Wu CJ, Azzolini AG, Dzhulgakov D. Deep learning recommendation model for personalization and recommendation systems. arXiv preprint arXiv:1906.00091. 2019 May 31.
[24] LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998 Nov;86(11):2278–324.
[25] W. A. Wulf and S. A. McKee, “Hitting the memory wall: Implications of the obvious,” ACM SIGARCH computer architecture news, vol. 23, no. 1, pp. 20–24, 1995.